TERC Blog
Authentically Integrating Mathematics into Making Experiences
While knowledge of mathematics is essential to every aspect of science, engineering, and technology, decades of research tell a consistent story: mathematics education in the United States is a barrier rather than a gateway to children’s engagement with STEM careers. Early in their lives, many children develop negative perceptions of mathematics and their own math abilities (Denner et al., 2019; Ganley & Lubienski, 2016; Jiang et al., 2020).
As mathematics becomes a more essential part of STEM classes and topics, these children can lose interest in STEM or doubt that they have the ability to pursue a STEM-related career (Cohen & Kelly, 2020; Dika & D’Amico, 2016; Jiang et al., 2020). To make matters worse, math in school is often portrayed as a disconnected set of formulas or procedures that have little to do with the creative, flexible ways that math is used in both STEM and our daily lives (Gutiérrez, 2018; NCTM, 2018; Pattison et al., 2017).
As STEM educators and researchers who have been working in the field of informal STEM education for many years, we believe that a key strategy for addressing these challenges is to rethink how mathematics is presented and thus expand the range of children and adults who see themselves as competent mathematical thinkers. One promising context for engaging new learners in mathematics lies in the growing maker movement across the country. At its core, “making” provides opportunities for individuals to take charge of their own learning, design and create based on their interests and passions, and develop their identities as STEM thinkers and doers (Calabrese Barton et al., 2017; Martin, 2015; Vossoughi & Bevan, 2014).1 We believe these making experiences are rich with opportunities for mathematical reasoning that often go unrecognized by both participants and educators.
Since 2015, we have been exploring this potential through the Math in the Making initiative. The work focuses particularly on children’s museums and science centers, many of which have developed maker spaces and programs over the last decade. In this article, we share insights from our most recent round of research. To begin, we consider the fundamental question of what it means to authentically integrate mathematics with making.
1 However, note these important critiques about equity and diversity in the maker movement (Tan et al., 2018; Vossoughi et al., 2016).
What is Authentic Integration?
A core commitment of the Math in the Making project has been to ensure that mathematics is integrated authentically into the making experience and is consequential to the goals of the maker. But what do we mean by “authentic integration”? How do we promote math reasoning and reflection without detracting from the freedom inherent in making experiences?
.jpg?width=509&name=Balancing%20Art%20(Copyright%20OMSI).jpg) Figure 1. Mobile sculpture exhibit highlighting the multiplicative relationship among weight, distance, and force on each side of the fulcrum.
Figure 1. Mobile sculpture exhibit highlighting the multiplicative relationship among weight, distance, and force on each side of the fulcrum.
As an example, first imagine that a middle school math teacher is working on a lesson on algebraic relationships. She has introduced the idea of balancing the two sides of an equation and is looking for a way to make this concept more intuitive. At the local science center, she saw a mobile sculpture exhibit that encouraged visitors to explore the multiplicative relationship among weight, distance, and force on each side of the fulcrum (see Figure 1). Working with educators from the museum, the teacher builds a smaller version of the balancing exhibit, with the distances and weights clearly marked so that her students can experiment with different weight-distance combinations. She even introduces the idea of a “mystery weight” that students must “solve for,” using the other weights in the balanced configuration. Through the process, the students engage in rich conversations about equations, variables, and multiplicative relationships.
Now imagine another scenario in which a middle school youth visits a maker space at her local science center. Inspired by sculptures she has seen and her own passion as an artist, she decides to create a balancing sculpture for the local community garden. However, she has trouble arranging her sculptural pieces so they balance correctly. With museum staff help, she discovers the relationship among weight, distance, and force that determines balance. Based on this research, she knows that she needs to hang the lighter sculptural piece about twice as far from the fulcrum as the heavier one. She then adjusts the arrangement until she achieves an overall balance that matches her artistic vision.
Both these examples depict rich math learning—one beginning with a core math concept and the other arising naturally as part of the making experience. Furthermore, both examples show the power of integrating math into hands-on, maker-related experiences. While neither of these approaches is necessarily better than the other, we are particularly interested in opportunities in which the mathematics arises naturally in service of goals set by the individual learner. These types of experiences can not only create a new perception of mathematics but also connect with a broader group of children and adults—highlighting their existing abilities as mathematical thinkers and sparking a renewed interest in math.
Our Own Maker Journey
There are few models of this authentic integration in the context of museum-based experiences. So, what might authentic integration look like? To explore this question, we partnered with the New York Hall of Science (NYSCI) and the Children’s Museum of Pittsburgh (CMP) to test ways of enhancing mathematical thinking and learning opportunities in museum-based making activities for families. From 2018 to 2021, we worked collaboratively with partners to refine our vision for authentic integration, identify promising making activities, design and test these activities using a variety of strategies, and synthesize lessons learned.
Our experiences with these activities led us to identify four potential design strategies for highlighting and enhancing their math potential, outlined in the adjacent box. Next, we describe how our work with two of these activities led to our articulation of these strategies.
- Curate materials to highlight salient mathematical relationships
- Tailor design choices so that mathematical issues are more likely to emerge
- Highlight mathematical quantities that are consequential to the making
- Incorporate materials and cues that visitors may see as math related
Weaving at the Children’s Museum of Pittsburgh
CMP’s MAKESHOP®, which caters to young children and their families, always features a full-sized loom with an in-process community fabric project. In addition to using the large loom, visitors can create their own looms by making a series of small cuts in parallel sides of a piece of cardboard and wrapping yarn around it to create a warp. They then start weaving, using the familiar over-under-over-under process (Figure 2a). Even in this simple activity, we saw children and families engage with patterns (alternating over/under). But how could we extend the mathematical thinking in this making experience for visitors?
The MAKESHOP at CMP is staffed by “teaching artists,” who are both educators and artists in their own right. Experienced weavers among the teaching artists noted two opportunities for mathematical reasoning in the process of weaving. The first recognized the reciprocal relationship between yarn thickness and the number of rows it takes to make a particular length of fabric. Thicker yarn makes weaving “go faster,” since it takes fewer rows to fill a space (Figure 2b). The second mathematical insight focused on creating geometrical shapes in a woven piece. Making a pattern like the one shown in Figure 2c, for example, requires making a series of increasing then decreasing rows of white and keeping track of how long each yellow row should be.



 Figure 2.
Figure 2.
(a) Weaving with a cardboard loom at CMP.
(b) The thicker the yarn, the fewer rows needed to fill a space.
(c) This diamond pattern requires a series of increasing then decreasing rows.
(d) Non-rectangular looms invite careful mathematical planning.
Once we recognized this potential, we still had to decide how to increase the likelihood that visitors would encounter these mathematical aspects of weaving in a compelling and authentically integrated way. To address the idea of yarn thickness, we made yarns of very different thicknesses available, so it would become obvious how those thicknesses affected the length of the resulting piece.
To introduce the mathematical complexity that arises when weaving a design that includes non-rectangular shapes, we made sure that there were examples of woven pieces with diagonal lines and curves visible to visitors. However, a more successful mathematical enhancement came from one of our museum partners: pre-made, non-rectangular looms. These looms require careful mathematical planning because each row may need a different number of over-under pairs than the previous one. A heart-shaped loom was particularly popular with visitors, as seen in Figure 2d.
Making these changes to the weaving activity at CMP helped us identify two promising design strategies for authentically integrating math and making:
- Curate materials to highlight salient mathematical relationships (e.g., yarn width)
- Tailor design choices so that mathematical issues are more likely to emerge (e.g., non-rectangular looms)
Fashion Design at the New York Hall of Science
Our colleagues at NYSCI were passionate about fashion design, since it was an activity they enjoyed themselves and one that attracted a wide variety of visitors, including both girls and boys (Figure 3). Although it seemed clear that sewing involves mathematics, we wanted to get beyond the obvious connection with measurement. The idea of scaling—working from a pattern that might not be the right size—seemed worth exploring. To limit the amount of material visitors would use, we decided to provide medium-sized dolls for visitors to dress. We hypothesized that the presence of the patterns would inspire visitors to consider using them for the dolls’ clothing while also signaling that there might be math involved in the process.

Figure 3. Mannequin dolls for the fashion design activity at NYSCI
Unfortunately, the COVID-19 pandemic temporarily closed the museum just as this activity was being readied for the floor. However, the NYSCI team was able to continue iterating on the idea of clothing design and mathematics in partnership with its NYSCI Neighbors program, which focuses on serving the museum’s highly diverse neighborhood in Queens. The Math in the Making project partnered with outreach staff to design a family mask-making workshop conducted over videoconference (Figure 4). Participating families received kits containing both practical materials for making masks, such as a tape measure and tape for fastening fabric, as well as materials for individualizing and decorating the masks, such as sequins. Families used scrap fabric they had at home, such as old T-shirts, to make the masks. The workshop focused on making child-sized masks, since most of the adults already had masks and well-fitting masks for children were hard to find at the time.

Figure 4. A child explores how a mask fits her mother in a virtual mask-making workshop.
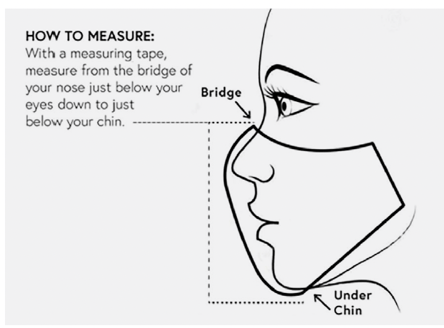
Figure 5. Measuring specific dimensions of the face is critical to ensure the mask fits snugly.
Families appeared to be highly engaged in the workshop, and many seemed to draw from their prior experience sewing and making clothes. Adults also seemed more aware that “math” was involved compared to other clothing design experiences facilitated by the museum. We observed families engaging in the mathematics inherent to the design process in a variety of ways—both through talk and gesture. Their math conversations seemed particularly motivated by the process of measuring specific dimensions of the face with the tape measure to ensure the mask would fit snugly, which made precise measurement consequential (Figure 5). These observations, and the team’s iterative testing of both the fashion design and mask-making activities, highlighted two additional design principles for authentically integrating math and making and helping visitors become more aware of their own mathematical reasoning:
- Highlight mathematical quantities that are consequential to the making (e.g., dimensions of face for fitting mask)
- Incorporate materials and cues that visitors may see as math-related (e.g., clothing patterns, measuring tape)
Conclusion
These stories represent just the beginning of our exploration into authentically integrating mathematics into making experiences—and using these experiences as an opportunity to help more children and adults see themselves as mathematical thinkers. We plan to use the design principles that emerged from our work as a starting point for additional research and the development of new programs and activities. Through this process, we hope to contribute to a more expansive vision of “doing mathematics” that resonates for all children and adults.
Additional Resources
Find out more about the Math in the Making initiative on the project website: www.terc.edu/mathinthemaking.
Acknowledgements
This work was conducted in close collaboration with our project partners and advisors, including Dorothy Bennett, Satbir Multani, Chip Lindsey, Rebecca Grabman, Alison Bank, Marta Civil, Peter Wardrip, and Debra Smith. The Math in the Making initiative was funded by the National Science Foundation under Grant No. 1514726 and 1811395. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Authors
Andee Rubin is a Senior Scientist at TERC with a background in math and computer science. She is committed to engaging people in the power of mathematics, especially data science, at all ages, both in and out of school.
Scott Pattison, Ph.D., is a Research Scientist at TERC. He partners with communities to study and support STEM education, learning, and interest development in free-choice and out-of-school environments, including museums, community-based programs, and everyday settings.
References
Calabrese Barton, A., Tan, E., & Greenberg, D. (2017). The makerspace movement: Sites of possibilities for equitable opportunities to engage underrepresented youth in STEM. Teachers College Record, 119(6), 1–44.
Cohen, R., & Kelly, A. M. (2020). Mathematics as a factor in community college STEM performance, persistence, and degree attainment. Journal of Research in Science Teaching, 57(2), 279–307. https://doi.org/10.1002/tea.21594
Denner, J., Valdes, O., Dickson, D. J., & Laursen, B. (2019). Math interest and self-concept among latino/a students: Reciprocal influences across the transition to middle school. Journal of Adolescence, 75, 22–36. https://doi.org/10.1016/j.adolescence.2019.06.015
Dika, S. L., & D’Amico, M. M. (2016). Early experiences and integration in the persistence of first-generation college students in STEM and non-STEM majors. Journal of Research in Science Teaching, 53(3), 368–383. https://doi.org/10.1002/tea.21301
Ganley, C. M., & Lubienski, S. T. (2016). Mathematics confidence, interest, and performance: Examining gender patterns and reciprocal relations. Learning and Individual Differences, 47, 182–193. https://doi.org/10.1016/j.lindif.2016.01.002
Gutiérrez, R. (2018). The need to rehumanize mathematics. In I. Goffney, R. Gutiérrez, & M. Boston (Eds.), Rehumanizing mathematics for black, indigenous, and latinx students (pp. 1–10). National Council of Teachers of Mathematics.
Jiang, S., Simpkins, S. D., & Eccles, J. S. (2020). Individuals’ math and science motivation and their subsequent STEM choices and achievement in high school and college: A longitudinal study of gender and college generation status differences. Developmental Psychology, 56(11), 2137–2151. https://doi.org/10.1037/dev0001110
Martin, L. (2015). The promise of the maker movement for education. Journal of Pre-College Engineering Education Research (J-PEER), 5(1), 30–39. https://doi.org/10.7771/2157-9288.1099
National Council of Supervisors of Mathematics & National Council of Teachers of Mathematics. (2018). Building STEM education on a sound mathematical foundation. https://www.nctm.org/Standards-and-Positions/Position-Statements/Building-STEM-Education-on-a-Sound-Mathematical-Foundation/
NCTM Research Committee. (2018). Asset-based approaches to equitable mathematics education research and practice. Journal for Research in Mathematics Education, 49(4), 373–389. https://doi.org/10.5951/jresematheduc.49.4.0373
Pattison, S. A., Rubin, A., & Wright, T. (2017). Mathematics in informal learning environments: A summary of the literature (updated). http://www.informalscience.org/mathematics-informal-learning-environments-summary-literature
Tan, E., Calabrese Barton, A., & Schenkel, K. (2018). Methods and strategies: Equity and the maker movement. Science and Children, 55(07). https://doi.org/10.2505/4/sc18_055_07_76
Vossoughi, S., & Bevan, B. (2014). Making and tinkering: A review of the literature. National Research Council Committee on Out of School Time STEM. Washington, DC: National Research Council, 1–55.
Vossoughi, S., Hooper, P. K., & Escudé, M. (2016). Making through the lens of culture and power: Toward transformative visions for educational equity. Harvard Educational Review, 86(2), 206–232. https://doi.org/10.17763/0017-8055.86.2.206