TERC Blog
Mathematical Argumentation, Open-ended Conjecturing, and Equity
Mathematical argumentation happens when students engage, as a classroom community of learners, in deciding together what is mathematically true or false. Argumentation has been integrated into many state standards over recent decades, and it can be—with the right supports—a practice that fosters creativity, inclusiveness, and equity. Yet it remains a new process for many teachers.
Our project team has developed professional development (PD) that aims to ease teachers and students into the argumentation process. In this article, we explain our model for middle-school argumentation, our PD model, and how they work to support equitable teaching practices.
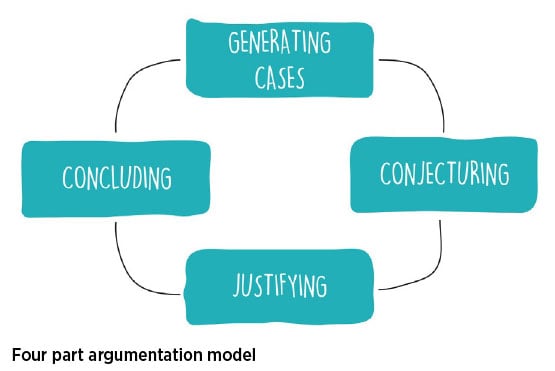
We define the four parts of argumentation as a vehicle for dividing classroom discourse into clearly defined phases. In our book Mathematical Argumentation in Middle School-The What, Why, and How (Knudsen, et al., 2017) we describe each phase:
-
Generating cases: creating something to argue about
-
Conjecturing: making bold claims
-
Justifying: building a chain of reasoning
-
Concluding: getting closure on truth or falsity
In practice, argumentation gets messier than that. For example, in a live classroom you might get rapid cycles of conjecturing and justifying, interspersed with new cases being generated. However, we’ve have found that these four phases are distinct enough to simplify the process for teachers and students new to argumentation.
Open-ended Conjecturing
Trying out conjecturing is a great way to get a feel for argumentation. In a recent webinar, as part of the National Council for Mathematics Teachers’ 100 Days of Professional Learning, our team engaged about 400 teachers in open-ended conjecturing—the process of a group making multiple, novel (to them) conjectures about a mathematical situation. We presented them with a table of numbers from 1 to 40 with a complete list of the factors of a number below it, and the square numbers highlighted in orange (see Table 1). The teachers were asked to make their best guesses about what might be true about all the whole numbers, up to and beyond 40. The numbers highlighted in orange offered starting points for successful conjecturing.
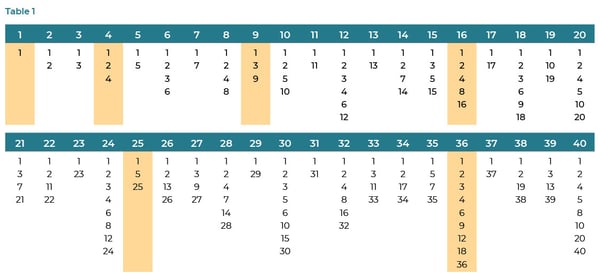
Below are three conjectures offered by the teachers, which though distinct, turn out to be related.
-
The square factor is the median of the factors listed.
-
Squares have an odd number of factors.
-
Non-squares have even numbers of factors.
How are these conjectures related? Take the first one: if you remember or look up the definition of median, you’ll quickly deduce that when the median of a data set is actually one of data points in that set, then the data set must contain an odd number of data points (otherwise the median is the average of two points). Here the data set is the list of factors. So, if the “square factor” of a number (the whole-number square root of that number) is on the list of factors, then that square number must have an odd number of factors. For example, 9 has the factors 1, 3, 9. Three is the middle number—the median. Three is the square root of 9. So, 9 is a square number and it has an odd number of factors. Of course, we can simply make this list of three factors for the number 9, to establish that 9, a perfect square number, has an odd number of factors. But in argumentation, we are searching for what always must be true—in this case, for any square number.
These three conjectures were made in the context of open-ended conjecturing, based on a mathematical situation or task that affords multiple conjectures. In practice, we recommend sticking to the conjecturing phase until quite a number of conjectures have been made, with a focus on what always might be true, and only then moving into justifying. Yet, in this particular example, the lines between conjecturing and justifying are blurred, because one conjecture can be used to justify another—that’s how it can work out in the classroom, too.
There are many other conjectures that can be made based on this table about square numbers, prime numbers, and even twin primes (with only one number between them). Try it yourself and have fun!
Of course, open-ended conjecturing is not just for teachers, but something we strongly advocate for students. The table of factors above comes from our book mentioned earlier (Corwin 2017) and is aimed at 6th graders. However, more commonly students are given single conjectures to justify: for example, “The product of two fractions less than one is smaller than either factor.” That’s a fine conjecture to explore. Opportunities for students to make their own conjectures, beyond a simple “agree” or “disagree”, are found less frequently, yet the open-ended process can yield rich results. For example, the table of factors has been successfully used online with 5th graders who were just beginning to understand the concept of factors.
Conjecturing for Equity
Why is open-ended conjecturing, and argumentation overall, considered to be supportive of classroom-level equity? One of the equitable teaching practices advocated by Aguirre, Mayfield-Ingram, and Martin (2013) is “going deeper with the mathematics.” Open-ended conjecturing is precisely how mathematics teachers and students can do this. A table of whole numbers can yield multiple, quite sophisticated conjectures—there were over 200 made at our presentation. The task offers multiple entry points: students can learn what a factor is from engaging in the task, considering the factors as a data set, or using algebraic symbols to express their conjectures (all entry points used by teachers in our presentation). These multiple entry points also help ensure equity, as students from different backgrounds, with different approaches and levels of entry-knowledge, can participate fully and creatively in the activity.
Scholars also promote creativity as a way to make mathematics more inclusive for students who are Black, Indigenous, or people of color (BIPOC) (Gutierrez, 2018). As well, helping students to speak up (in this case, to give voice to their own conjectures) supports students’ mathematical agency, which is key to classroom equity (Cobb & Hodge, 2007). Our PD provides strategies for teachers to support students to use their voices, improvise creatively, and go deeper into mathematics.

Games and Improvisations for Teaching Moves and Norms
Engaging students in all four parts of argumentation— from a set of cases, to conjectures about them, to justifications of the conjectures, to stating general conclusions—can be challenging. It requires a specialized set of teaching moves and norms. That’s what our PD is designed for: to help teachers establish norms and develop teaching moves that support students’ participation in argumentation.
Our current PD model includes a series of successive “approximations of practice” (Grossman, et al, 2009): engaging in mathematical argumentation as learners; choosing teaching moves to support argumentation among students; playing “teaching games” to try out and practice new moves; and engaging in “visualization planning.” This sequence enables teachers to slowly acquire expertise in new practices.
Two activities unique to our PD model are teaching games and visualization planning.
Teaching games (Knudsen & Shechtman, 2016) are akin to activities that improvisational theater performers use to learn their craft. We provide well-specified rules to bound teaching moves that are improvisationally deployed. A teacher and their peers play out part of an argumentation lesson, with a facilitator observing. The game is then discussed to determine the usefulness and challenges of the particular moves that were in play.
Open- and Closed-Ended Questions
In this game, teachers are given a conjecture to justify.
- In the first round they are allowed to ask only open-ended questions, such as “Why do you think so?”
- In the second round, they may ask only closed-ended questions, such as “Which numbers on the list are square numbers?”
After both rounds, teachers compare the advantages and limitations of each type of question. In live conjecturing in the classroom, we suggest teachers use both types, not just one. This game helps them to know the potential purposes of each.
Visualization planning is a process that pairs a teacher and another teacher, the teacher’s coach, or a PD leader. They choose a part of an argumentation lesson on which to focus. The teacher sits back and imagines out loud how that part of the lesson might go, anticipating questions they might ask and students’ likely responses. Their partner asks probing questions, helping the teacher envision different routes the lesson might take. The partner also records the imagining in a lesson-planning form that the teacher can take away and elaborate on.
Our PD makes unique use of “improv” games as metaphors for social and socio-mathematical norms—the norms that set a productive atmosphere for argumentation and that students must share in order to work collaboratively as a community of mathematicians on an argument (Nussbaum, 2008). Improv games provide a way to internalize norms through experiential learning, in a way more likely to “stick” than simply by placing them on a poster on the wall. To demonstrate, let’s look at a game called Gift Giving.
Gift Giving*
In this game, players work in pairs.
- The first player reaches into an imaginary closet, pulls out an imaginary wrapped gift, and presents it to the second player.
- The second player takes it, unwraps its elaborate imaginary packaging, announces what it is, and thanks the first player.
- The first player has to accept whatever the second player says the gift is and explain why it was specially chosen for the recipient.
After playing this game, one teacher told her class that “a conjecture is like a gift” (Knudsen, et al, 2014, 2017). She said that when you get a new conjecture, it may be unfamiliar, but you don’t reject it. You take it and see how you can work with it. In this way, playing and discussing the game helps students internalize the classroom norm, “Accept all conjectures in the conjecturing phase of argumentation.”
* This game can be found in Knudsen (2017). This and many improv games were drawn from the collective corpus that improvisational actors use to learn their craft.
Establishing norms through improv games is also a practice for fostering classroom-level equity. Socio-mathematical norms might be already known and practiced by some members of the class, but not by others (Herbel-Eisenmann., Choppin, Wagner, & Pimm, 2011))—in many cases BIPOC youth, whose experiences in argumentation, while no less relevant to the classroom community, may come with different norms.
The model of argumentation and PD model summarized here were developed over 15 years of research, teacher interactions, and classroom observation. Our current project, Visualize Teaching, will use both these models but extend them to content coaching and to more mathematical practices, such as seeing and using structure. Visualize Teaching also includes video-based coaching, where teachers capture video of their class engaged in argumentation and discuss it with their coaches, providing a clear window onto their practices. The first Visualize Teaching PD is coming up in the summer of 2021, and we are excited to see how teachers and coaches work together with these tools. Learn more at terc.edu/viste/

Download Hands On! Fall 2020
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant Nos. DRL-14178950, DRL-1417895, and DRL-1119518. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Harriette S. Stevens, Teresa Lara-Meloy, Nicole Shechtman, Hee-Joon Kim, Ken Rafanan, and Phil Vahey all had important roles in developing the methods presented in this article. We are grateful to all the teachers and students involved in the projects, from whom we learned so much.
Author
Jennifer Knudsen is a mathematics educator whose work is at the crossroads of research and design. A veteran curriculum and professional development designer, Knudsen has led many projects, from mathematical argumentation to 3D modeling and printing for learning mathematics and computational thinking.
References
Aguirre, J., Mayfield-Ingram, K., & Martin, D. (2013). The impact of identity in K-8 mathematics: Rethinking equity-based practices. The National Council of Teachers of Mathematics.
Cobb, P., & Hodge, L. (2007). Culture, identity, and equity in mathematics classrooms. In N. S. Nasir & P. Cobb (Eds.), Improving access in mathematics: Diversity and equity in the classroom (pp. 159–172). Teachers College Press.
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055-2100.
Herbel-Eisenmann, B., Choppin, J., Wagner, D., & Pimm, D. (Eds.). (2011). Equity in discourse for mathematics education: Theories, practices, and policies (Vol. 55). Springer Science & Business Media.
Knudsen, J., Lara-Meloy, T., Stevens, H. S., & Rutstein, D. W. (2014). Advice for mathematical argumentation. Mathematics Teaching in the Middle School, 19(8), 494-500.
Knudsen, J., & Shechtman, N. (2016). Professional development that bridges the gap between workshop and classroom through disciplined improvisation. In S. Goldman & Z. Kabayadondo (Eds.), Taking design thinking to school: How the technology of design can transform teachers, learners, and classrooms (163). Routledge.
Knudsen, J., Stevens, H. S., Lara-Meloy, T., Kim, H. J., Schechtman, N., & Shechtman, N. (2017). Mathematical Argumentation in Middle School-The What, Why, and How: A Step-by-Step Guide With Activities, Games, and Lesson Planning Tools. Corwin Press.
Nussbaum, E. M. (2008). Collaborative discourse, argumentation, and learning: Preface and literature review. Contemporary Educational Psychology, 33(3), 345-359.
Gutierrez, R. Why do we need to humanize mathematics? Annual Perspectives in Mathematics Education 2018. Edited by Imani Goffney and Rochelle Gutiérrez.
For free TERC math resources, click here.






.jpeg)

-Bonda.jpg)